Despre Frank Benford și legea lui

Anton Kovacs – www.infokam.ro

Intr-o propunere pe care o făcusem guvernului sugeram că cei care fraudează sistemul ar putea fi depistați comparând cifrele raportate către instituțiile statului cu o distribuție Benford.

Sunt însă aproape sigur că aproape nimeni din cei care au citit propunerea respectivă nu a înțeles despre ce este vorba.

Cred însă că este totuși util, cel puțin pentru cultura noastră generală, să aflăm cum cineva poate fi prins că raportează date false, nu legând casele de marcat la cine știe ce supersistem informatic care este aproape sigur că nu va funcționa, nici terorizând vânzătoarele din butică cu tot felul de idioți mascați, ci pur și simplu uitându-se la niște date pe un monitor. De aceea am să povestesc în continuare câte ceva despre acest subiect, fără a intra în prea multe detalii, care probabil ar fi neinteresante pentru marea majoritate a cititorilor:

Frank Benford a fost un fizician american care, în 1938 a descoperit că primele cifre dintr-un șir de numere preluat din lumea reală respectă următoarea proporție:

Acest lucru se întâmplă pentru că lumea reală nu este “construită” după o scală liniară, în care “distanța” dintre 1 și 2 ar fi egală cu o zecime a distanței de la 1 la 10, ci după una logaritmică (numai la acest lucru și la implicațiile care rezultă ne putem gândi o întregă viață), de aceea în lumea reală valoarea proporției P(d) între două numere care fac parte dintr-un dintr-un șir d este proporțională cu spațiul dintre d și d+1 într-o scală logaritmică, adică

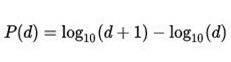Dacă înlocuim, de exemplu  valoarea lui d cu 1, deci vom avea d+1=2, și cunoscând că valoarea logaritmului zecimal al lui 1 este 0 și logaritmul zecimal a lui 2 este 0.301 vom afla că distanța în lumea naturală și reală între 1 și 2 este de 0.301-0=0.301, deci numerele care încep cu 1 trebuie să se regăsească într-o mulțime în proporție de 30.1%, la fel ca în tabelul de mai sus.

sau, presupunând că d=8 și știind că logaritmul zecimal al lui 8 este 0.90308, iar logaritmul zecimal al lui d+1, adică 8+1=9 este 0.95424, nu trebuie decât să facem diferența și aflăm că “distanța” într-o scală logaritmică dintre 8 și 9 este de 0.051, ceea ce înseamnă că într-o listă de numere generate de cauze naturale cele care încep cu 8 se regăsesc într-o proporție de 5.1%

Cât se poate de clar. nu-i așa?

Mai târziu “Legea lui Benford” a fost popularizată de Mark Nigrini, un profesor de contabilitate, care a folosit-o pentru a detecta anomaliile din tabelele cu care lucra (exact ce vom face și noi mai jos).

In prezent Legea lui Benford este folosită de o mulțime de instituții din toată lumea, pentru detectarea fraudelor cu ocazia alegerilor, a fraudelor din lucrările științifice, cercetare, statistică, arhitectură și multe altele. Metoda este folosită în unele țări și pentru detectarea fraudelor fiscale, exemplul cel mai popular fiind vestitul IRS din SUA.

S-a observat (prea târziu) că dacă datele macroeconomice raportate de Grecia înainte de aderarea la UE ar fi fost analizate pe baza Legii lui Benford s-ar fi constatat falsitatea acestora.

Un șir de numere din lumea reală poate fi orice șir de numere destul de mare pentru a fi semnificativ și care nu este direct influențat de către o anumită persoană. De exemplu, greutatea câinilor dintr-un oraș oarecare va respecta regulile enunțate de Benford. La fel se va întâmpla cu înălțimea oamenilor dintr-un oraș, înălțimea caselor dintr-o localitate, înălțimea copacilor sau numărul de frunze din acei copaci, valoarea mărfurilor cumpărate dintr-un magazin într-un anumit interval etc.

Exemplificând tabelul de mai sus putem spune că dacă luăm la mână 1000 de bonuri de casă dintr-un supermarket, o categorie de magazin care vinde produse cu o multitudine de prețuri, ar fi normal ca sumele înscrise pe 301 din aceste bonuril să înceapă cu cifra 1, 176 să înceapă cu cifra 2, 125 să înceapă cu cifra 3 și așa mai departe, ajungănd ca numai 4.6% din bonuri să aibe înscrise valori între 9 lei și 9.99 lei, între 90 lei și 99.99 lei sau între 900  și 999.99 lei.

La fel se va întâmpla și dacă cântărim 1000 de câini, 301 din ei vor avea 1kg sau între 11 și 19 kg, 176 vor avea 2 kg sau între 21 și 29 kg, 125 vor avea 3 kg sau între 31 și 39 kg, etc.

In ciuda faptului că pare puțin mistică, regula asta totuși funcționează și funcționează bine, de aceea se numește “Legea lui Benford” și nu “părerea lui Benford”. Iată niște teste care dovedesc acest lucru:

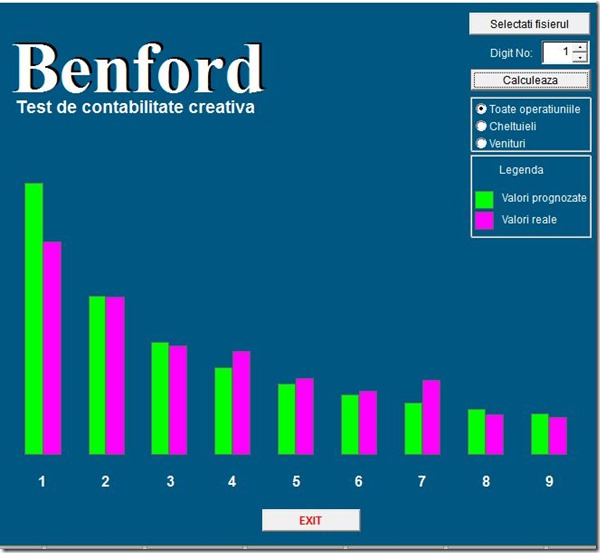
Aici puteți vedea cum arată cifrele din contabiilitatea unei firme (toate sumele înscrise în 5 ani în  Registrul Jurnal), comparate cu distribuția Benford. După cum puteți observa cifrele reale aproape că se suprapun peste cele prognozate (cifrele nu respectă “perfect” legea pentru că intervin și influențe “nenaturale”, vindem la anumite prețuri pe care uneori le fixăm arbitrar din cosiderente de adaptare la piață sau din considerente pshihologice (un exemplu în acest sens sunt prețurile de genul 3.99), cumpărăm numai anumite produse etc, de aceea când facem analize de acest gen va fi necesar să acceptăm o mică marjă de eroare):

Aici se poate vedea distribuția prețurilor dintr-o listă care cuprinde câteva mii de repere, din nou legea lui Benford se verifică:

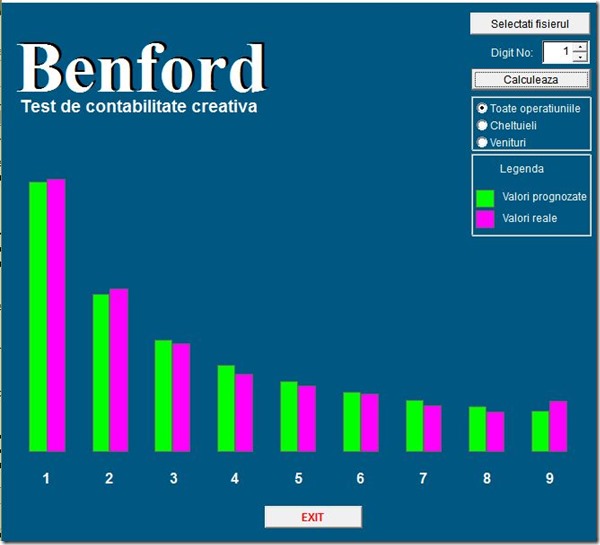Trebuie însă să fim atenți cum folosim această lege, există situații în care, chiar dacă apar diferențe foarte mari între prognoză și datele analizate, acestea din urmă să fie totuși corecte.

De exemplu, în cazul de mai jos marea majoritate a valorii vânzărilor se încadrează în plaja 201-299 lei, ceea ce e normal când vinzi o gamă foarte limitată de produse sau servicii care fac parte din aceeași categorie.

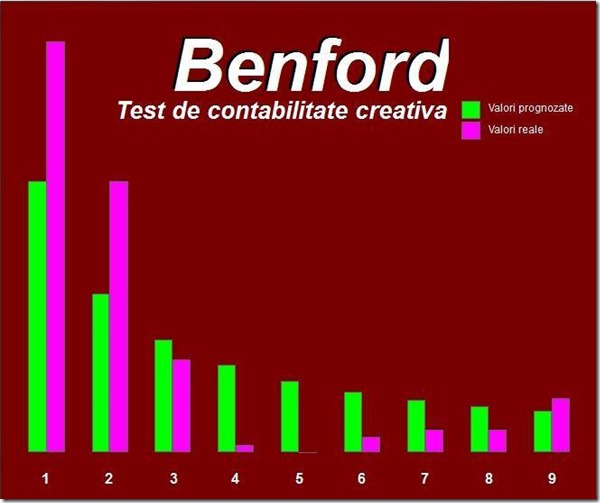
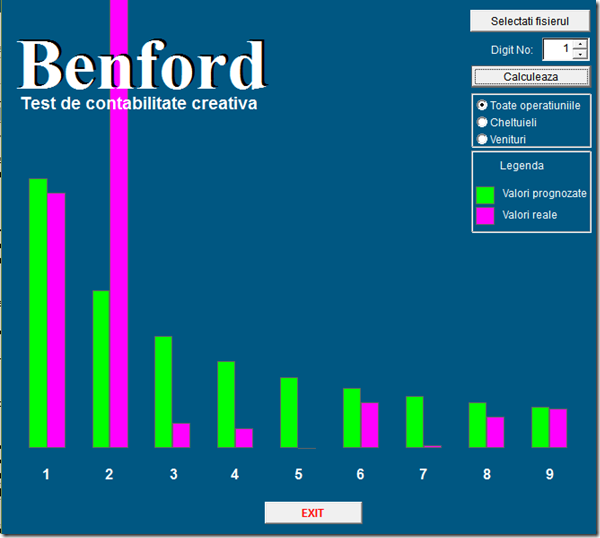Iată însă o dovadă clară de fraudă, comparația greutății câinilor care se afirmă că au fost prinși și sterilizați într-un an de către hingherii unui mare oraș din România și distribuția Benford:

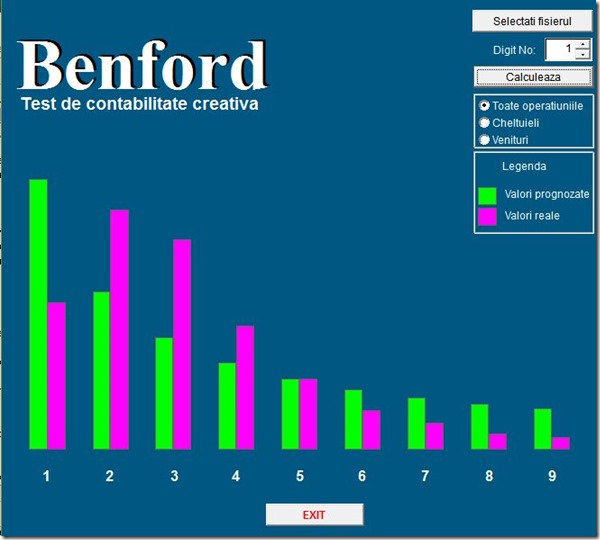
Sau, comparația cu distribuția Benford a unei liste de prețuri ale unor medicamente, prețuri care este clar că nu au nici o legătură cu realitatea ci au fost “puse din burtă”:

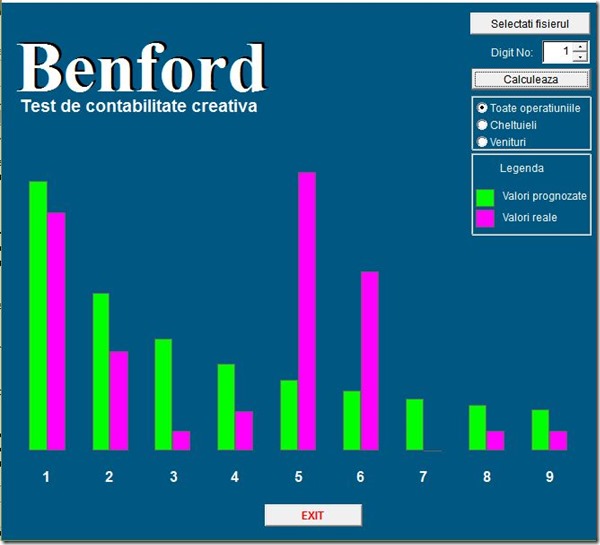Din nou o dovadă clară de fraudă, omul mergea pur și simplu la benzinărie în fiecare zi și cerea un bon de vreo 40 de lei Probabil că dacă cifrele ar fi reflectat consumul real ar fi fost mai multe bonuri în valoare de 10 și 20 lei și mult mai puține cele de 40 lei.

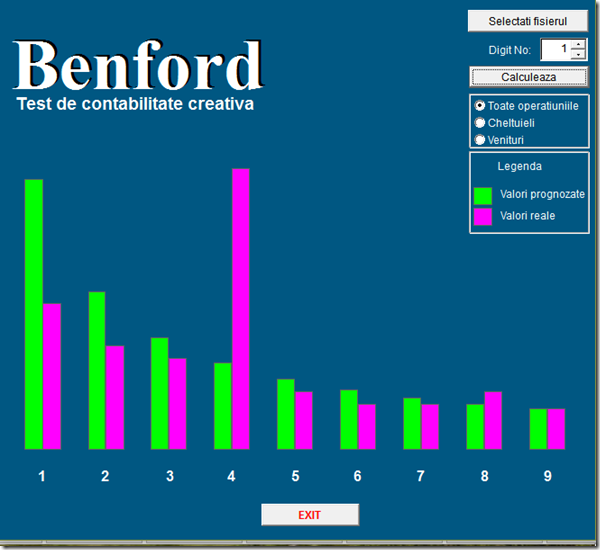Si în final, cel de la butica din colț care probabil bate doar din când în când câte ceva pe casa de marcat, să nu spună lumea că “lucrează la negru”. E posibil să fie fraudă sau există o mică probabilitate să fie pur și simplu o întâmplare. Dar, dacă numele meu ar fi ANAF aș face un mic semn în dreptul ăstuia pentru a-l urmări mai atent pe viitor.

Bibliografie: Bendord’s Law – Wikipedia